1 CONSISTENCY TEST OF RECIPROCAL MATRIX OF PAIRWISE COMPARISON
The important point is that the expected rank of A (if A is consistent) is 1and the expected eigenvalue is equal to the number of compared criteria (n). In inconsistent cases, the expected maximum eigenvalue is greater than n while the others are close to zero. The eigenvector of matrix A is an estimate of the relative weights of the criteria being compared.
In ideal cases the comparison matrix (A) is fully consistent, the rank(A) = 1 and ë = n (n = number of criteria). In this case, the following equation is valid:
A × x = n × x (where x is the eigenvector of A)
In the inconsistent cases (which are more common) the comparison matrix A may be considered as a perturbation of the previous consistent case. When the entries aij changes only slightly, then the eigenvalues change in a similar fashion. Moreover, the maximum eigenvalue (ëmax) is slightly greater than n while the remaining (possible) eigenvalues are close to zero. Thus in order to find weights, we are looking for the eigenvector that corresponds to the maximum eigenvalue (ëmax).
The consistency index (CI) is calculated as follows
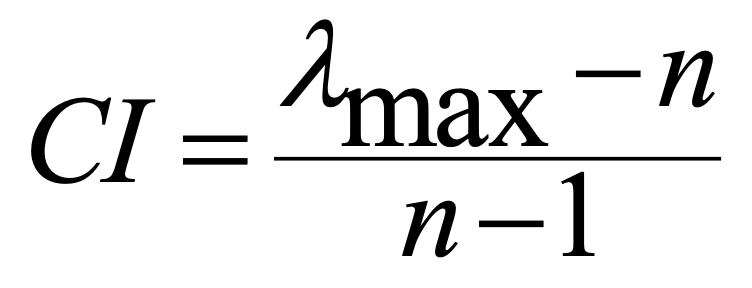
22.
Then, the consistency ratio (CR) is calculated as the ratio of consistency index and random consistency index (RI). The RI is the random index representing the consistency of a randomly generated pairwise comparison matrix It is derived as an average random consistency index (Table 4) calculated from a sample of 500 of randomly generated matrices based on the AHP scale.
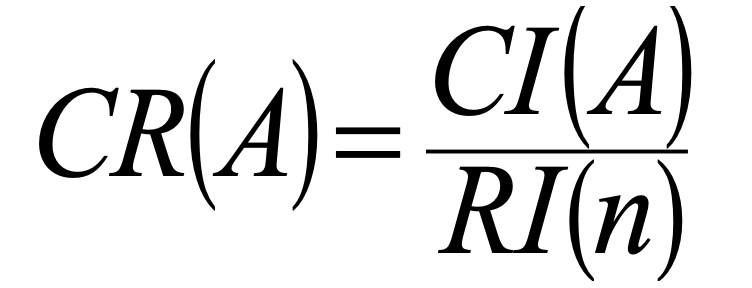
23.
If CR(A) ≤ 0.1, the pairwise comparison matrix is considered to be consistent enough. In the case CR(A) ≥ 0.1, the comparison matrix should be improved. The value of RI depends on the number criteria being compared.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| RCI | 0 | 0 | 0.58 | 0.9 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
